Πόσο μακριά μπορείτε να δείτε έναν μετεωρίτη;
>Παίρνω email.
Οι περισσότεροι κάνουν ερωτήσεις διαφόρων τύπων, οι περισσότερες από τις οποίες είναι αρκετά απλές στην απάντηση (στην πραγματικότητα, πολλά θα μπορούσαν να απαντηθούν με το googling, υπόδειξη υπόδειξης). Αλλά μερικές φορές παίρνω μια ερώτηση που είναι πιο δύσκολο να απαντήσω, ή ακόμα και μια που έχω αναρωτηθεί για τον εαυτό μου, αλλά δεν έχω φτάσει ποτέ να το καταλάβω.
Έτσι, με ενθουσίασε πολύ όταν έλαβα μια ερώτηση από τον Bad Reader Dean Lewis σχετικά με τους μετεωρίτες. Κατά τη διάρκεια της βροχής μετεωριτών Perseid το 2018 ήταν μακριά από την οικογένειά του, χωρισμένος με περίπου 1.000 χιλιόμετρα. Αν έβλεπε έναν μετεωρίτη, ήταν δυνατόν να μπορούσαν να δουν τον ίδιο από την πιο μακρινή περιοχή τους;
Η σύντομη απάντηση είναι: Ναι! Η μεγάλη απάντηση είναι ... μαθηματικά. Δροσερά, διασκεδαστικά μαθηματικά.
Και βλέποντας πώς, όταν δημοσιεύεται αυτό το άρθρο, η ετήσια βροχή μετεωριτών Geminid 2018 κορυφώνεται απόψε, νομίζω ότι είναι σκόπιμο να το καταλάβουμε.
ημερολόγιο μιας εφηβικής κοπέλας κριτική
Crash Course Astronomy: Meteors, Meteoroids, and Meteorites, Oh My!
Εάν η Γη ήταν απόλυτα επίπεδη, τότε καταρχήν θα μπορούσατε να δείτε έναν μετεωρίτη μέχρι την άκρη της Γης. Όσο βρίσκεστε πάνω από το έδαφος, έστω και λίγο έφηβοι, τότε η οπτική σας γωνία φτάνει σε κάθε τετραγωνικό εκατοστό του πλανήτη από την πλευρά σας, έτσι κάθε μετεωρίτης είναι ορατός σε όλους. Στην πραγματικότητα, ο αέρας δεν είναι απόλυτα διαφανής, οπότε σε κάποια απόσταση ψάχνετε τόσο πολύ που δεν μπορείτε να δείτε τίποτα.
Ωστόσο, η Γη δεν είναι επίπεδη. Σοβαρά! Είναι στρογγυλό. Και η ατμόσφαιρα το περιβάλλει σαν κοχύλι, γίνεται πιο λεπτή με το ύψος και τελικά ξεφεύγει. αυτό το ύψος εξαρτάται από τον ορισμό του χώρου. Ωστόσο, μπορούμε να απατήσουμε λίγο αφού γνωρίζουμε την επιστήμη: Μετεωρίτες όπως αυτοί που βρέχονται τείνουν να καίγονται περίπου 100 χιλιόμετρα πάνω από το έδαφος. Αυτό το ύψος εξαρτάται από πολλά πράγματα, συμπεριλαμβανομένου του πόσο μεγάλο είναι μετεωροειδή (τα συμπαγή κομμάτια των διαπλανητικών συντριμμιών που διαπερνούν το διάστημα) είναι, πόσο γρήγορα κινούνται, σε ποια γωνία εισέρχονται στην ατμόσφαιρα κ.ο.κ. Ας το πούμε όμως 100 χιλιόμετρα.
Το πιο κοντινό που μπορεί να είναι ένας μετεωρίτης είναι εάν βρίσκεστε ακριβώς κάτω από αυτό, και στη συνέχεια είναι 100 χιλιόμετρα ευθεία (στο ζενίθ σας). Εάν καίγεται πιο μακριά από το ζενίθ, τότε πρέπει να είναι πιο μακριά από εσάς. Το πιο μακριά που μπορείτε να δείτε έναν μετεωρίτη, είναι λογικό, είναι, επομένως, εάν βρίσκεται ακριβώς στον ορίζοντα.
Η γεωμετρία του μοιάζει με αυτήν (σημείωση: ΟΧΙ σε κλίμακα):
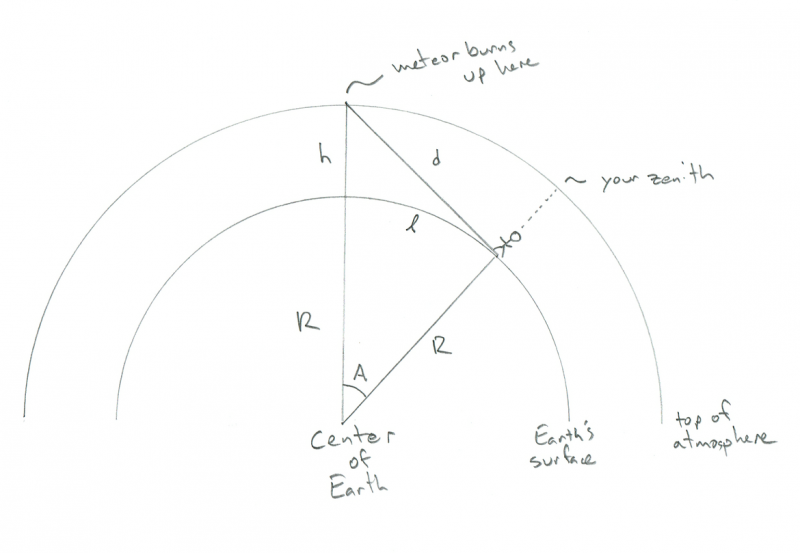
Σχηματική απεικόνιση της γεωμετρίας ενός παρατηρητή που παρακολουθεί έναν μετεωρίτη να καίγεται. Πίστωση: Phil Plait
Μπορείτε να δείτε τη φιγούρα του ανθρώπου να στέκεται στην επιφάνεια της καμπύλης Γης - ας πούμε ότι είστε εσείς - με την (επίσης καμπύλη) ατμόσφαιρα πάνω τους. Σε αυτό το διάγραμμα, R είναι η ακτίνα της Γης (6.4000 km), h είναι το ύψος που καίει ο μετεωρίτης (100 km) και d είναι η απόσταση από εσάς μέχρι τον μετεωρίτη. Α είναι η γωνία μεταξύ της θέσης σας στη Γη και της θέσης του μετεωρίτη πάνω από αυτήν, και η περιληπτική λ (όπως και στο μήκος) είναι η απόσταση που πρέπει να περπατήσετε για να είναι ο μετεωρίτης ακριβώς πάνω από το κεφάλι (ξέρω ότι φαίνεται σαν ένα περίεργο πράγμα να θέλω να μάθω, αλλά άντεξε με). Παραδόξως, μπορείτε να υπολογίσετε όλα όσα χρειάζεστε εδώ χωρίς να γνωρίζετε d, αλλά ελάτε, είναι ωραίο να γνωρίζετε πόσο μακριά είναι ο μετεωρίτης, σωστά;
Το κλειδί για όλα αυτά είναι να δούμε ότι η γωνία μεταξύ του μετεωρίτη, εσάς και του κέντρου της Γης είναι ορθή γωνία. Αυτό συμβαίνει επειδή ο μετεωρίτης βρίσκεται στον ορίζοντα όπως τον είδατε (ή, αν προτιμάτε τη διασκεδαστική ορολογία, στην εφαπτομένη γραμμή στον εσωτερικό κύκλο όπου το τέμνει το R). Αυτό κάνει το τρίγωνο ορθογώνιο τρίγωνο, και αν θυμάστε τα μαθηματικά στο λύκειο, αυτό σημαίνει ότι μπορείτε να βρείτε όλες τις πλευρές και τις γωνίες!
Θυμάμαι το Πυθαγόρειο θεώρημα ; Σε ένα ορθογώνιο τρίγωνο, το τετράγωνο του μήκους της υποτείνουσας είναι ίσο με το άθροισμα των τετραγώνων των άλλων δύο πλευρών*. Στο τρίγωνό μας, η υποτείνουσα είναι R+h και οι άλλες πλευρές είναι R και d.
Έτσι
(R+h)2= δ2+ R2
ή, πολλαπλασιάζοντας την αριστερή πλευρά (χρήση ΑΛΟΥΜΙΝΟΧΑΡΤΟ ):
R2+ 2Rh + h2 = d2+ R2
Λύστε το για να δείτε πόσο μακριά είναι ο μετεωρίτης από εσάς. Σημειώστε ότι το R2 βρίσκεται και στις δύο πλευρές, οπότε ακυρώστε τα για να το αποκτήσετε
ρε2= 2Rh + h2
Ή
d = τετραγωνική ρίζα (2Rh + h2)
Λοιπόν, γνωρίζουμε όλους αυτούς τους αριθμούς! Plug-n-chug, μωρό μου:
d = τετραγωνική ρίζα (2 x 6.400 x 100 + 10.000) = 1.136 km
Αχα! Αυτό σημαίνει ότι αν δείτε έναν μετεωρίτη στον ορίζοντα, είναι πάνω από 1.100 χιλιόμετρα μακριά! Αυτό είναι μακρύς δρόμος, και τεχνικά το πιο μακρυά μπορείτε να δείτε έναν μετεωρίτη από το έδαφος.
Τώρα ας βρούμε αναλυτικό l. Πρώτα πρέπει να γνωρίζουμε τη γωνία Α. Αυτό απαιτεί κάποια τριγωνομετρία. Υπάρχουν πολλά τριγωνικές ταυτότητες μπορείτε να το χρησιμοποιήσετε για να το καταλάβετε, αλλά το αγαπημένο μου†είναι ότι σε ορθογώνιο τρίγωνο, το ημίτονο μιας γωνίας είναι το μήκος της αντίθετης πλευράς διαιρούμενο με το μήκος της υποτείνουσας. Έτσι, αν λάβουμε αυτήν την αναλογία, μπορούμε να πάρουμε το αντίστροφο ημίτονο (ή τόξο) για να πάρουμε τη γωνία.
αμαρτία (A) = d / (R + h)
Έτσι
Α = χωρίς-1(d / R + h)
Plug-n-chug ξανά και παίρνω A = 10 °. Αυτό είναι ένα αξιοπρεπές κομμάτι της επιφάνειας της Γης!
Και τώρα μπορούμε να πάρουμε αναλυτικά l. Υπάρχουν 360 ° γύρω από τη Γη και η περιφέρεια της Γης είναι 2 x pi x ακτίνα = 40.192 km, άρα υπάρχουν
40.192 χλμ. / 360 ° = 112 χιλιόμετρα ανά βαθμό
που σημαίνει, με τη σειρά του, 10 ° = 1.120 χιλιόμετρα. Αυτό είναι πολύ κοντά στο d, κάτι που δεν προκαλεί έκπληξη. Τα σχέδια είναι υπερβολικά, αλλά στην πραγματικότητα το κέλυφος του αέρα πάνω μας είναι μικρό σε σύγκριση με το μέγεθος της Γης. Αν έκανα τα σχέδια σε κλίμακα θα έβλεπες ότι το d και το l είναι πραγματικά πολύ κοντά σε μήκος.
Εντάξει, γιατί είμαι τόσο καυτός και ενοχλημένος που βρήκα; Λόγω της αρχικής ερώτησης! Αν ξεχάσατε μετά από όλα αυτά τα μαθηματικά, είναι πόσο μακριά μπορούν να είναι δύο άνθρωποι και να βλέπουν τον ίδιο μετεωρίτη;
Λοιπόν, σε αυτή την περίπτωση, ο μετεωρίτης θα ήταν ακριβώς μεταξύ τους, και σε κάθε έναν από τους αντίστοιχους ορίζοντές τους. Αυτή η γεωμετρία μοιάζει με αυτό:
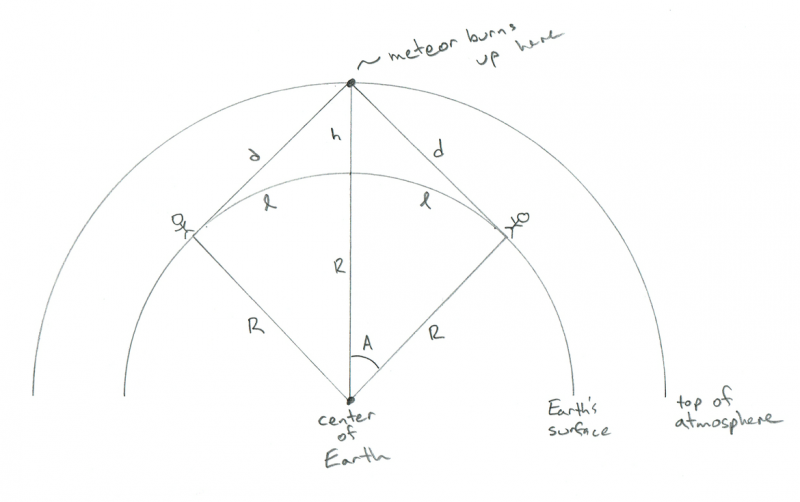
Σχηματική απεικόνιση της γεωμετρίας δύο παρατηρητών που παρακολουθούν έναν μετεωρίτη να καίγεται ακριβώς μεταξύ τους. Πίστωση: Phil Plait
ΑΧΑ! Τώρα βλέπεις γιατί το θέλω! Η απόσταση μεταξύ των δύο ατόμων είναι μόλις 2 x l! Τώρα λοιπόν έχουμε την απάντηση:
Για να δουν δύο άτομα τον ίδιο μετεωρίτη, δεν μπορούν να απέχουν μεταξύ τους περισσότερο από 2 x 1.120 = 2.240 χιλιόμετρα. Για παράδειγμα, αυτό είναι πολύ κοντά στην απόσταση μεταξύ Ουάσιγκτον, DC και Ντένβερ. Ουάου.
γιατί η Παρασκευή το 13ο βαθμολογείται r
Παρεμπιπτόντως, για αλλαγή προοπτικής (κυριολεκτικά), αυτό σημαίνει από την άποψη του μετεωρίτη, μπορεί να δει ένα τμήμα της Γης πλάτους 2.240 χιλιομέτρων (όπως, DC στο ανατολικό άκρο της Γης και το Ντένβερ στο δυτικό). Αυτό είναι πολύ ωραίο.
Και αυτό μας φέρνει στην πραγματική απάντηση στην ερώτηση του Dean: Αν ήταν 1.000 χιλιόμετρα από την οικογένειά του, τότε ναι, τεχνικά θα μπορούσαν να δουν τον ίδιο μετεωρίτη. Τι λέτε για αυτό;
Τώρα αυτό υποθέτει και πάλι ότι ο αέρας είναι απόλυτα διαυγής και όλα αυτά, τα οποία στην πραγματικότητα είναι ουσιαστικά αδύνατα. Έτσι αυτά τα μαθηματικά αντιπροσωπεύουν μια ιδανική κατάσταση (συμπεριλαμβανομένης της ιδέας ότι ο μετεωρίτης βρίσκεται ακριβώς μεταξύ τους).
Ας γίνουμε πιο ρεαλιστές. Ας πούμε ότι ο μετεωρίτης καίγεται στον ουρανό σε υψόμετρο 45 ° πάνω από τον ορίζοντα και για τους δύο παρατηρητές. Πόσο μακριά θα ήταν ο ένας από τον άλλο; Λοιπόν, και πάλι υποθέτοντας ότι ο μετεωρίτης βρίσκεται ακριβώς μεταξύ τους, η γεωμετρία μοιάζει περισσότερο με αυτήν:
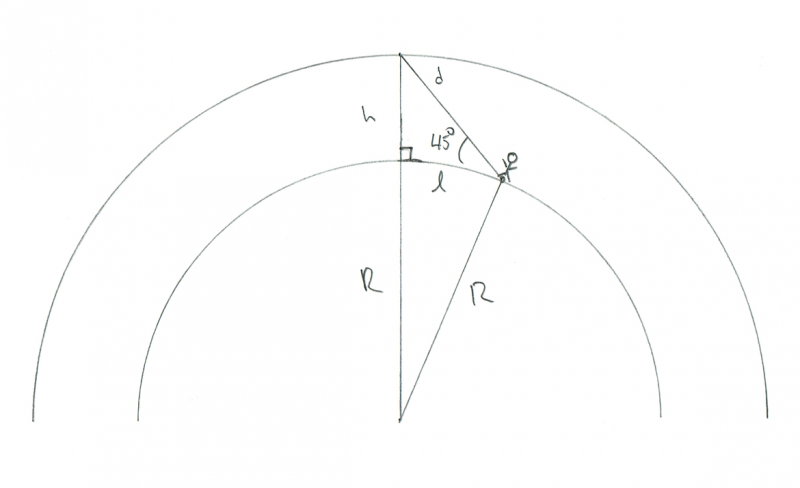
Σχηματική απεικόνιση της γεωμετρίας ενός παρατηρητή που παρακολουθεί έναν μετεωρίτη να καίγεται 45 ° πάνω από τον ορίζοντα. Πίστωση: Phil Plait
Αυτό είναι πραγματικά πιο δύσκολο να λυθεί, αλλά ξέρω ένα άλλο κόλπο: Αν υποθέσουμε ότι το l είναι μικρό, τότε η καμπυλότητα της Γης δεν θα είναι σημαντική. Για παράδειγμα, αν θέλω να μάθω την απόσταση μεταξύ δύο δέντρων στην αυλή μου, δεν με νοιάζει που η Γη είναι καμπύλη. Σε μια τόσο μικρή απόσταση μπορώ να υποθέσω ότι είναι επίπεδη. Ας κάνουμε αυτήν την υπόθεση εδώ.
Σε αυτή την περίπτωση, έχουμε ένα άλλο ορθογώνιο τρίγωνο, αλλά αυτή τη φορά η σωστή γωνία είναι αυτή κάτω από τον μετεωρίτη. Το χαρακτήρισα ακόμη και στο διάγραμμα με το μικρό τετράγωνο συμβολικό πράγμα. Αν λοιπόν αυτή είναι γωνία 90 ° και η γωνία μας με τον μετεωρίτη είναι 45 °, τότε η τελευταία γωνία (από τον μετεωρίτη στον παρατηρητή) είναι επίσης 45 °. Αυτό σημαίνει ότι αυτό πρέπει να είναι ένα ισοσκελές τρίγωνο, οπότε το l και το h είναι το ίδιο! Δεδομένου ότι γνωρίζουμε ότι το h είναι 100 χιλιόμετρα, έτσι πρέπει και το l.
Και αυτό σημαίνει ότι η απόσταση μεταξύ των δύο παρατηρητών μας είναι διπλάσια, ή 200 χιλιόμετρα.
Παρεμπιπτόντως, σε αυτή την περίπτωση η απόσταση από τον μετεωρίτη είναι περίπου 141 χιλιόμετρα. Θα το αφήσω επιβεβαιώνοντας ως άσκηση στον αναγνώστη.
Κατ 'αρχήν, αυτό σημαίνει ότι εάν γνωρίζετε πόσο ψηλά βρίσκεται στον ορίζοντα ένας μετεωρίτης και το ύψος στο οποίο κάηκε, μπορείτε να υπολογίσετε την απόστασή του (ή εάν γνωρίζετε την απόσταση μπορείτε να πάρετε το ύψος του). Αυτό το τρίγωνο είναι αρκετά περίπλοκο, όμως, και νομίζω ότι σας έριξα αρκετά μαθηματικά για σήμερα.
Αλλά είναι ωραίο να πιστεύουμε ότι λίγα μαθηματικά γυμνασίου μπορούν να έχουν μια τόσο διασκεδαστική εφαρμογή. Και θα παραδεχτώ ότι είναι ποιητικό και ρομαντικό να γνωρίζεις ότι, εφόσον ο χωρισμός δεν είναι πολύ μακριά, είναι δυνατό να μοιραστείς το να βλέπεις ένα αστέρι που σκοπεύει με κάποιον άλλο. Τι υπέροχη σκέψη.
* Σε Ο μάγος του Οζ , το σκιάχτρο το έκανε λάθος μετά πήρε εγκέφαλο.
† Του σειρά μαθημάτων Έχω μια αγαπημένη τριγωνική ταυτότητα. Τι είναι δικό σου?